Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.

Yandex.RTB R-A-339285-1

Необходимо дать определение точкам пересечения двух прямых.

Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать, быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.

Определение точки пересечения прямых звучит так:

Определение 1

Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.

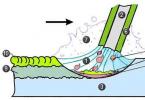
Рассмотрим на рисунке, приведенном ниже.

Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.

Если на плоскости имеется система координат О х у, то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b - A 2 x + B 2 y + C 2 = 0 . Тогда M 0 (x 0 , y 0) является некоторой точкой плоскости необходимо выявить, будет ли точка М 0 являться точкой пересечения этих прямых.

Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 (x 0 , y 0) считается их точкой пересечения.

Пример 1

Даны две пересекающиеся прямые 5 x - 2 y - 16 = 0 и 2 x - 5 y - 19 = 0 . Будет ли точка М 0 с координатами (2 , - 3) являться точкой пересечения.

Решение

Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что

5 · 2 - 2 · (- 3) - 16 = 0 ⇔ 0 = 0 2 · 2 - 5 · (- 3) - 19 = 0 ⇔ 0 = 0

Оба равенства верные, значит М 0 (2 , - 3) является точкой пересечения заданных прямых.

Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами (2 , - 3) будет являться точкой пересечения заданных прямых.

Пример 2

Пересекутся ли прямые 5 x + 3 y - 1 = 0 и 7 x - 2 y + 11 = 0 в точке M 0 (2 , - 3) ?

Решение

Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что

5 · 2 + 3 · (- 3) - 1 = 0 ⇔ 0 = 0 7 · 2 - 2 · (- 3) + 11 = 0 ⇔ 31 = 0

Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x - 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.

Чертеж наглядно показывает, что М 0 - это не точка пересечения прямых. Они имеют общую точку с координатами (- 1 , 2) .

Ответ: точка с координатами (2 , - 3) не является точкой пересечения заданных прямых.

Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.

Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у. При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .

Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .

Значит, для нахождения координат точки пересечения, необходимо все уравнения добавить в систему и решить ее.

Пример 3

Заданы две прямые x - 9 y + 14 = 0 и 5 x - 2 y - 16 = 0 на плоскости. необходимо найти их пересечение.

Решение

Данные по условию уравнения необходимо собрать в систему, после чего получим x - 9 y + 14 = 0 5 x - 2 y - 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:

x - 9 y + 14 = 0 5 x - 2 y - 16 = 0 ⇔ x = 9 y - 14 5 x - 2 y - 16 = 0 ⇔ ⇔ x = 9 y - 14 5 · 9 y - 14 - 2 y - 16 = 0 ⇔ x = 9 y - 14 43 y - 86 = 0 ⇔ ⇔ x = 9 y - 14 y = 2 ⇔ x = 9 · 2 - 14 y = 2 ⇔ x = 4 y = 2

Получившиеся числа являются координатами, которые необходимо было найти.

Ответ: M 0 (4 , 2) является точкой пересечения прямых x - 9 y + 14 = 0 и 5 x - 2 y - 16 = 0 .

Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.

Пример 4

Определить координаты точек пересечения прямых x - 5 = y - 4 - 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .

Решение

Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:

x = 4 + 9 · λ y = 2 + λ ⇔ λ = x - 4 9 λ = y - 2 1 ⇔ x - 4 9 = y - 2 1 ⇔ ⇔ 1 · (x - 4) = 9 · (y - 2) ⇔ x - 9 y + 14 = 0

После чего беремся за уравнение канонического вида x - 5 = y - 4 - 3 и преобразуем. Получаем, что

x - 5 = y - 4 - 3 ⇔ - 3 · x = - 5 · y - 4 ⇔ 3 x - 5 y + 20 = 0

Отсюда имеем, что координаты – это точка пересечения

x - 9 y + 14 = 0 3 x - 5 y + 20 = 0 ⇔ x - 9 y = - 14 3 x - 5 y = - 20

Применим метод Крамера для нахождения координат:

∆ = 1 - 9 3 - 5 = 1 · (- 5) - (- 9) · 3 = 22 ∆ x = - 14 - 9 - 20 - 5 = - 14 · (- 5) - (- 9) · (- 20) = - 110 ⇒ x = ∆ x ∆ = - 110 22 = - 5 ∆ y = 1 - 14 3 - 20 = 1 · (- 20) - (- 14) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1

Ответ: M 0 (- 5 , 1) .

Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .

Пример 5

Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x - 5 = y - 4 - 3 .

Решение

Необходимо выполнить подстановку в x - 5 = y - 4 - 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:

4 + 9 · λ - 5 = 2 + λ - 4 - 3

При решении получаем, что λ = - 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x - 5 = y - 4 - 3 . Для вычисления координат необходимо подставить выражение λ = - 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · (- 1) y = 2 + (- 1) ⇔ x = - 5 y = 1 .

Ответ: M 0 (- 5 , 1) .

Для полного понимания темы, необходимо знать некоторые нюансы.

Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.

Пример 6

Даны прямые x 3 + y - 4 = 1 и y = 4 3 x - 4 . Определить, имеют ли они общую точку.

Решение

Упрощая заданные уравнения, получаем 1 3 x - 1 4 y - 1 = 0 и 4 3 x - y - 4 = 0 .

Следует собрать уравнения в систему для последующего решения:

1 3 x - 1 4 y - 1 = 0 1 3 x - y - 4 = 0 ⇔ 1 3 x - 1 4 y = 1 4 3 x - y = 4

Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y - 4 = 1 и y = 4 3 x - 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.

Ответ: заданные уравнения определяют одну и ту же прямую.

Пример 7

Найти координаты точки пересекающихся прямых 2 x + (2 - 3) y + 7 = 0 и 2 3 + 2 x - 7 y - 1 = 0 .

Решение

По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:

2 x + (2 - 3) y + 7 = 0 2 (3 + 2) x - 7 y - 1 = 0 ⇔ 2 x + (2 - 3) y = - 7 2 (3 + 2) x - 7 y = 1 ⇔ ⇔ 2 x + 2 - 3 y = - 7 2 (3 + 2) x - 7 y + (2 x + (2 - 3) y) · (- (3 + 2)) = 1 + - 7 · (- (3 + 2)) ⇔ ⇔ 2 x + (2 - 3) y = - 7 0 = 22 - 7 2

Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.

Второй способ решения.

Для начала нужно определить наличие пересечения прямых.

n 1 → = (2 , 2 - 3) является нормальным вектором прямой 2 x + (2 - 3) y + 7 = 0 , тогда вектор n 2 → = (2 (3 + 2) , - 7 - нормальный вектор для прямой 2 3 + 2 x - 7 y - 1 = 0 .

Необходимо выполнить проверку коллинеарности векторов n 1 → = (2 , 2 - 3) и n 2 → = (2 (3 + 2) , - 7) . Получим равенство вида 2 2 (3 + 2) = 2 - 3 - 7 . Оно верное, потому как 2 2 3 + 2 - 2 - 3 - 7 = 7 + 2 - 3 (3 + 2) 7 (3 + 2) = 7 - 7 7 (3 + 2) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.

Ответ: точек пересечения нет, прямые параллельны.

Пример 8

Найти координаты пересечения заданных прямых 2 x - 1 = 0 и y = 5 4 x - 2 .

Решение

Для решения составляем систему уравнений. Получаем

2 x - 1 = 0 5 4 x - y - 2 = 0 ⇔ 2 x = 1 5 4 x - y = 2

Найдем определитель основной матрицы. Для этого 2 0 5 4 - 1 = 2 · (- 1) - 0 · 5 4 = - 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:

2 x = 1 5 4 x - y = 2 ⇔ x = 1 2 4 5 x - y = 2 ⇔ x = 1 2 5 4 · 1 2 - y = 2 ⇔ x = 1 2 y = - 11 8

Получили, что точка пересечения заданных прямых имеет координаты M 0 (1 2 , - 11 8) .

Ответ: M 0 (1 2 , - 11 8) .

Нахождения координат точки пересечения двух прямых в пространстве

Таким же образом находятся точки пересечения прямых пространства.

Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b - A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .

Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0

Рассмотрим подобные задания на примерах.

Пример 9

Найти координаты точки пересечения заданных прямых x - 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x - 2 z - 4 = 0

Решение

Составляем систему x - 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x - 2 z - 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 - 2 и расширенную T = 1 0 0 1 0 1 2 - 3 4 0 - 2 4 . Определяем ранг матрицы по Гауссу.

Получаем, что

1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = - 4 ≠ 0 , 1 0 0 1 0 1 2 - 3 3 2 0 - 3 4 0 - 2 4 = 0

Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x - 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x - 27 - 4 = 0 в результате дает только одно решение.

Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = - 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x - 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x - 2 z - 4 = 0 ⇔ x = 1 y + 2 z = - 3 3 x + 2 y - 3 . Решение системы x = 1 y + 2 z = - 3 3 x + 2 y = - 3 ⇔ x = 1 y + 2 z = - 3 3 · 1 + 2 y = - 3 ⇔ x = 1 y + 2 z = - 3 y = - 3 ⇔ ⇔ x = 1 - 3 + 2 z = - 3 y = - 3 ⇔ x = 1 z = 0 y = - 3 .

Значит, имеем, что точка пересечения x - 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x - 2 z - 4 = 0 имеет координаты (1 , - 3 , 0) .

Ответ: (1 , - 3 , 0) .

Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.

В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.

Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.

Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.

Пример 10

Заданы уравнения прямых x + 2 y - 3 z - 4 = 0 2 x - y + 5 = 0 и x - 3 z = 0 3 x - 2 y + 2 z - 1 = 0 . Найти точку пересечения.

Решение

Для начала составим систему уравнений. Получим, что x + 2 y - 3 z - 4 = 0 2 x - y + 5 = 0 x - 3 z = 0 3 x - 2 y + 2 z - 1 = 0 . решаем ее методом Гаусса:

1 2 - 3 4 2 - 1 0 - 5 1 0 - 3 0 3 - 2 2 1 ~ 1 2 - 3 4 0 - 5 6 - 13 0 - 2 0 - 4 0 - 8 11 - 11 ~ ~ 1 2 - 3 4 0 - 5 6 - 13 0 0 - 12 5 6 5 0 0 7 5 - 159 5 ~ 1 2 - 3 4 0 - 5 6 - 13 0 0 - 12 5 6 5 0 0 0 311 10

Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.

Ответ: нет точки пересечения.

Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.

Пример 11

Заданы две прямые x = - 3 - λ y = - 3 · λ z = - 2 + 3 · λ , λ ∈ R и x 2 = y - 3 0 = z 5 в О х у z . Найти точку пересечения.

Решение

Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что

x = - 3 - λ y = - 3 · λ z = - 2 + 3 · λ ⇔ λ = x + 3 - 1 λ = y - 3 λ = z + 2 3 ⇔ x + 3 - 1 = y - 3 = z + 2 3 ⇔ ⇔ x + 3 - 1 = y - 3 x + 3 - 1 = z + 2 3 ⇔ 3 x - y + 9 = 0 3 x + z + 11 = 0 x 2 = y - 3 0 = z 5 ⇔ y - 3 = 0 x 2 = z 5 ⇔ y - 3 = 0 5 x - 2 z = 0

Находим координаты 3 x - y + 9 = 0 3 x + z + 11 = 0 y - 3 = 0 5 x - 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 - 1 0 3 0 1 0 1 0 = - 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что

3 x - y + 9 = 0 3 x + z + 11 = 0 y - 3 = 0 5 x - 2 z = 0 ⇔ 3 x - y + 9 = 0 3 x + z + 11 = 0 y - 3 = 0

Решим систему методом Крамер. Получаем, что x = - 2 y = 3 z = - 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами (- 2 , 3 , - 5) .

Ответ: (- 2 , 3 , - 5) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

С помощю этого онлайн калькулятора можно найти точку пересечения прямых на плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых ("канонический", "параметрический" или "общий"), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку "Решить". Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Очистить все ячейки?

Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Точка пересечения прямых на плоскости − теория, примеры и решения

1. Точка пересечения прямых, заданных в общем виде.

Oxy L 1 и L 2:

Построим расширенную матрицу:

Если B" 2 =0 и С" 2 =0, то система линейных уравнений имеет множество решений. Следовательно прямые L 1 и L 2 совпадают. Если B" 2 =0 и С" 2 ≠0, то система несовместна и, следовательно прямые параллельны и не имеют общей точки. Если же B" 2 ≠0, то система линейных уравнений имеет единственное решение. Из второго уравнения находим y : y =С" 2 /B" 2 и подставляя полученное значение в первое уравнение находим x : x =−С 1 −B 1 y . Получили точку пересечения прямых L 1 и L 2: M (x, y ).

2. Точка пересечения прямых, заданных в каноническом виде.

Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L 1 и L 2:

Откроем скобки и сделаем преобразования:

Аналогичным методом получим общее уравнение прямой (7):

Из уравнений (12) следует:

Как найти точку пересечения прямых, заданных в каноническом виде описано выше.

4. Точка пересечения прямых, заданных в разных видах.

Найдем t :

A 1 x 2 +A 1 m t +B 1 y 2 +B 1 p t +C 1 =0,

Решим систему линейных уравнений отностительно x, y . Для этого воспользуемся методом Гаусса . Получим:

Пример 2. Найти точку пересечения прямых L 1 и L 2:

L 1: 2x +3y +4=0,

(20)

(21)

Для нахождения точки пересечения прямых L 1 и L 2 нужно решить систему линейных уравнений (20) и (21). Представим уравнения в матричном виде.

Тема 3. Теория

Аналитическая геометрия в пространстве.

Уравнения плоскости и прямой линии.

 Общее уравнение плоскости является алгебраическим уравнением первого порядка относительно координат (x ; y ; z )

- нормаль , вектор, перпендикулярный плоскости.

Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормалей.

Некоторые стандартные виды уравнений плоскости:

	Уравнение плоскости, перпендикулярной вектору , проходящей через данную точкуМ 0 (х 0 , y 0 , z 0 )	A(x-x 0 )+B(y-y 0 )+C(z-z 0 )=0
	Плоскость, проходящая через три заданные точки М 1 (х 1 , y 1 , z 1 ) , M 2 (x 2 , y 2 , z 2 ) , M 3 (x 3 , y 3 , z 3 )
	Параллельная двум заданным векторам и , (неколлинеарный), проходящим через точкуМ 0 (х 0 , y 0 , z 0 )
	Проходящая через две заданные точки М 1 и М 2 , параллельно вектору , (неколлинеарный )
	Проходящая через заданную точку М 0 (x 0 , y 0 , z 0 ) , перпендикулярно двум заданным плоскостям: A 1 x+B 1 y+C 1 z+D 1 =0 ; A 2 x+B 2 y+C 2 z+D 2 =0 .

Собственно уравнения плоскости будут получены, если раскрыть соответствующий определитель по первой строке.

 Формула для вычисления расстояния от заданной точки М 1 (x 1 , y 1 , z 1 ) до плоскости , заданной уравнением Ах+ By + Cz + D =0 :

Очевидно, если d =0 , то точка М 1 принадлежит плоскости.

 Прямая линия в пространстве определяется как линия пересечения двух не параллельных плоскостей (любых, проходящих через прямую).

Виды уравнений прямой в пространстве:

		Общие уравнения прямой (пересечение двух плоскостей)
	, М 0 (x 0 , y 0 , z 0 ) – любая точка, лежащая на прямой. -направляющий вектор прямой	Канонические уравнения прямой или уравнения прямой, проходящей через заданную точку с заданным направляющим вектором
		Параметрическое уравнение
		Уравнения прямой, проходящей через две заданные точки М 1 и М 2

Условия параллельности и перпендикулярности прямых в пространстве определяются как условия соответственно коллинеарности и перпендикулярности их направляющих векторов. Пусть прямые (1) и (2) заданы в каноническом или параметрическом виде, тогда

.

 Условие пересечения двух прямых в пространстве – это условие комплонарности трех векторов:

 Переход от общих уравнений прямой к уравнениям в каноническом или параметрическом виде осуществляется следующим образом (возможен и обратный переход).

Заданы уравнения прямой в общем виде:
.

Найдем координаты направляющего вектора:
как векторное произведение нормалей плоскостей, задающих прямую.

Найдем любую точку, принадлежащую прямой. Она также принадлежит обеим плоскостям, задающим прямую, поэтому ее координаты (x 0 , y 0 , z 0) можно найти из системы уравнений:

в которой одну из координат надо задать произвольно (т.к. находим любую точку), но так, чтобы система имела единственное решение. Координаты вектора и найденной точки подставляют в канонические или параметрические уравнения.

Условия параллельности и перпендикулярности прямой и плоскости формулируют как условия перпендикулярности и параллельности нормали и направляющего вектора.

Al+Bm+Cn=0.

Пусть даны две прямые и требуется найти их точку пересечения. Так как эта точка принадлежит каждой из двух данных прямых, то ее координаты должны удовлетворять как уравнению первой прямой, так и уравнению второй прямой.

Таким образом, для того чтобы найти координаты точки пересечения двух прямых, следует решить систему уравнений

Пример 1. Найти точку пересечения прямых и

Решение. Координаты искомой точки пересечения мы найдем, решив систему уравнений

Точка пересечения М имеет координаты

Покажем, как построить прямую по ее уравнению. Для построения прямой достаточно знать две ее точки. Чтобы построить каждую из этих точек, мы задаемся произвольным значением одной из ее координат, а затем из уравнения находим соответствующее значение другой координаты.

Если в общем уравнении прямой оба коэффициента при текущих координатах не равны нулю , то для построения этой прямой лучше всего находить точки ее пересечения с осями координат.

Пример 2. Построить прямую .

Решение. Находим точку пересечения данной прямой с осью абсцисс. Для этого решаем совместно их уравнения: