Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Продолжим знакомиться с геометрическими алгоритмами. На прошлом уроке мы нашли уравнение прямой линии по координатам двух точек. У нас получилось уравнение вида:
Сегодня мы напишем функцию, которая по уравнениям двух прямых линий будет находить координаты их точки пересечения (если такая имеется). Для проверки равенства вещественных чисел, будем использовать специальную функцию RealEq().
Точки на плоскости описываются парой вещественных чисел. При использовании вещественного типа операции сравнения лучше оформить специальными функциями.
Причина известна: на типе Real в системе программирования Паскаль нет отношения порядка, поэтому записи вида a = b, где a и b вещественные числа, лучше не использовать.
Сегодня мы введем в употребление функцию RealEq() для реализации операции “=” (строго равно) :
Function RealEq(Const a, b:Real):Boolean; {строго равно} begin RealEq:=Abs(a-b)<=_Eps End; {RealEq}
Задача. Заданы уравнения двух прямых: и . Найти точку их пересечения.
Решение. Очевидное решение состоит в том, чтобы решить систему уравнений прямых: 
Давайте перепишем эту системе несколько иначе:
(1)
Введем обозначения: , 
, 
. Здесь D – определитель системы, а - определители, получающиеся в результате замены столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Если , то система (1) является определенной, то есть имеет единственное решение. Это решение можно найти по следующим формулам: , , которые называются формулами Крамера
. Напомню, как вычисляется определитель второго порядка. В определителе различают две диагонали: главную и побочную. Главная диагональ состоит из элементов, взятых по направлению от верхнего левого угла определителя в нижний правый угол. Побочная диагональ – из правого верхнего в нижний левый. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
В программном коде для проверки проверка равенства используется функция RealEq(). Вычисления над вещественными числами производятся с точностью до _Eps=1e-7.
Program geom2; Const _Eps: Real=1e-7;{точность вычислений} var a1,b1,c1,a2,b2,c2,x,y,d,dx,dy:Real; Function RealEq(Const a, b:Real):Boolean; {строго равно} begin RealEq:=Abs(a-b)<=_Eps End; {RealEq} Function LineToPoint(a1,b1,c1,a2,b2,c2: real; var x,y:real):Boolean; {Определение координат точки пересечения двух линий. Значение функции равно true, если точка пересечения есть, и false, если прямые параллельны. } var d:real; begin d:=a1*b2-b1*a2; if Not(RealEq(d,0)) then begin LineToPoint:=True; dx:=-c1*b2+b1*c2; dy:=-a1*c2+c1*a2; x:=dx/d; y:=dy/d; end else LineToPoint:=False End;{LineToPoint} begin {main} writeln("Введите коэффициенты уравнений: a1,b1,c1,a2,b2,c2 "); readln(a1,b1,c1,a2,b2,c2); if LineToPoint(a1,b1,c1,a2,b2,c2,x,y) then writeln(x:5:1,y:5:1) else writeln("Прямые параллельны."); end.
Мы составили программу, с помощью которой можно, зная уравнения линий, найти координаты их точки пересечения.
Перпендикулярная прямая
Это задача наверное одна из самых популярных и востребованных в школьных учебниках. Задачи, основанные на эту тему многообразны. Это и определение точки пересечения двух прямых, это и определение уравнения прямой, проходящяя через точку на исходной прямой под каким либо углом.
Эту тему мы раскроем, используя в своих вычислениях данные полученные с помощью
Именно там было рассмотрено преобразование общего уравнения прямой, в уравнение с угловым коэффициентом и обратно, и определения остальных парметров прямой по заданным условиям.
Что же нам не хвататет для того, что бы решать те задачи, которым посвящена эта страница?
1. Формулы вычисления одного из углов между двумя пересекающимися прямыми.
Если мы имеем две прямые которые заданы уравнениями:
то один из углов вычисляется так:
2. Уравнение прямой с угловым коэффициентом, проходящяя через заданную точку
Из формулы 1, мы можем увидеть два пограничных состояния
а) когда тогда и следовательно эти две заданные прямые паралельны (или совпадают)
б) когда , тогда , и следовательно эти прямые перпендикулярны, то есть пересекаются под прямым углом.
Какие могут быть исходные данные для решения подобных задач, кроме заданной прямой?
Точка на прямой и угол под которым вторая прямая его пересекает
Второе уравнение прямой
Какие же задачи может позволить решить бот?
1. Заданы две прямые (явным или не явным образом например по двум точкам). Вычислить точку пересечения и углы по которыми они пересекаются.
2. Задана одна прямая, точка на прямой и один угол. Определить уравнение прямой, перескающую заданную под указанным углом
Примеры
Две прямые заданы уравнениями. Найти точку пересечения этих прямых и углы под которым они пересекаются
line_p A=11;B=-5;C=6,k=3/7;b=-5
Получаем следующий результат
Уравнение первой прямой
y = 2.2 x + (1.2)
Уравнение второй прямой
y = 0.4285714285714 x + (-5)
Угол пересечения двух прямых(в градусах)
-42.357454705937
Точка пересечения двух прямых
x = -3.5
y = -6.5
Не забудьте что параметры двух линий разделяются запятой, а параметры каждой линии точкой с запятой.
Прямая проходит через две точки (1:-4) и (5:2) . Найти уравнение прямой, которая проходит через точку (-2:-8) и пересекает исходную прямую под углом 30 градусов.
Одна прямая нам известна, так как известны две точки через которые она проходит.
Осталось определить уравнение второй прямой. Одна точка нам известна, а вместо второй указан угол, под которым первая прямая пересекает вторую.
Вроде все известно, но тут главное не ошибится. Речь идет об угле(30 градусов) не между осью абсцисс и линией, а между первой и второй линией.
Для этого мы постим так. Определим параметры первой линии, и узнаем под каким углом она пересекает ось абсцисс.
line xa=1;xb=5;ya=-4;yb=2
Общее уравнение Ax+By+C = 0
Коэффициент А = -6
Коэффициент B = 4
Коэффициент C = 22
Коэффициент a= 3.6666666666667
Коэффициент b = -5.5
Коэффициент k = 1.5
Угол наклона к оси (в градусах) f = 56.309932474019
Коэффициент p = 3.0508510792386
Коэффициент q = 2.5535900500422
Расстояние между точками=7.211102550928
Видим что первая линия пересекает ось под углом 56.309932474019 градусов.
В искходных данных не сказано как именно пересекает вторая линия, первую. Можно ведь построить две линии удовлетворяющих условиям, первая повернутая на 30 градусов ПО часовой стрелке, а вторая на 30 градусов ПРОТИВ часовой стрелке.
Давайте их и посчитаем
Если вторая линия повернута на 30 градусов ПРОТИВ часовой стрелке, то вторая линия будет иметь градус пересечения с осью абсцисс 30+56.309932474019 = 86 .309932474019 градусов
line_p xa=-2;ya=-8;f=86.309932474019
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C = 0
Коэффициент А = 23.011106998916
Коэффициент B = -1.4840558255286
Коэффициент C = 34.149767393603
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a= -1.4840558255286
Коэффициент b = 23.011106998916
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k = 15.505553499458
Угол наклона к оси (в градусах) f = 86.309932474019
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p = -1.4809790664999
Коэффициент q = 3.0771888256405
Расстояние между точками=23.058912962428
Расстояние от точки до прямой li =
то есть наше уравнение второй линии есть y=15.505553499458x + 23.011106998916
Комментариев 11
Задача
Найти точку пересечения двух прямых отложенных от двух точек с известными координатами и азимутов от этих точек.
Применение
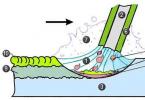
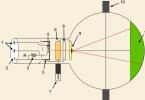
Для изучения поведения животных часто используют радиотелеметрический метод: исследуемый объект помечается радиопередатчиком, который испускает радиосигнал определенной частоты и далее исследователь при помощи приемника и принимающей антенны следит за перемещениями этого объекта. Одним из возможных способов определения точного местоположения объекта является метод биангуляции. Для этого исследователю требуется взять 2 азимута на исследуемый объект с точек с известными координатами. Местоположение объекта будет соответствовать точке пересечения этих двух азимутов. Координаты точек, с которых засекаются азимуты можно снять с помощью спутникового навигатора (GPS), либо азимуты снимаются с реперных точек, координаты которых известны заранее. Азимут в этом случае – направление на источник наиболее сильного сигнала, исходящего от меченного передатчиком объекта, измеряемое обычно в градусах.
Перед расчетами необходимо точки полученные с помощью GPS перевести в спроецированную систему координат, например соответствующую зону UTM, это можно сделать с помощью DNRGarmin .
Для того чтобы рассчитанное местоположение исследуемого объекта наиболее точно соответствовало реальному положению нужно учитывать следующее:
1) необходимо стараться дождаться момента, чтобы ошибка определения координат в навигаторе была как можно меньше.
2) чтобы угол между азимутами стремился к 90 градусам (по крайней мере, был больше 30 и меньше 150 градусов).
Расстояние, с которого следует снимать азимут, зависит от дальности действия передатчика, при этом применяется эмпирическое правило, что погрешность в определении азимута увеличивается на 1 метр с удалением от исследуемого объекта на каждые 10 м. Т.о. при снятии азимута с расстоянием до объекта 100 м погрешность составит 10 м. Однако, это правило применимо на ровной открытой местности. Следует учитывать, что неровности рельефа и древесно-кустарниковая растительность экранируют и отражают сигнал. Следует избегать нахождения в непосредственной близости от исследуемого объекта, т.к. во-первых, слишком сильный сигнал затруднит определение точного азимута, а, во-вторых, в некоторых случаях будет невозможно рассчитать точку пересечения из-за того, что второй азимут будет проходить за точкой снятия первого азимута. Временной интервал между снятием пары азимутов должен быть минимизирован, но, конечно, зависит от подвижности исследуемого животного.
Решение
Задача решается с помощью простейшей геометрии и решения
системы уравнений.
Для начала из точки и азимута получаем уравнение прямой, для этого:
Из уравнения общего вида:
ax + by + c = 0
при условии, что b<>0 получаем
y = kx + d , где k=-(a/b) , d=-(c/b)
таким образом, получаем
k=tan(a)
d=y-tan(a)*x
b=1
k1x + d1 = y
k2x + d2 = y
Получаем координаты X и Y общей точки двух прямых (точки пересечения).
В уравнении необходимо предусмотреть два особых случая, когда прямые параллельны (k1=k2).
Так как мы имеем дело не с векторами и не с лучами, то есть у линий нет начала и конца, то так же необходимо предусмотреть случай пересечения прямых вне области интереса, т.н. ложное пересечение. Решение этой задачи достигается измерением азимута из ложной точки a3 на точку 2, если азимут a3 = a2, то пересечение ложное, обратный азимут от полученной точки обратно на исходные 2 не должен быть равен одному из исходных азимутов.
Необходимая процедура на языке Avenue выглядит так:
a1rad = (90-a1)*pi/180a2rad = (90-a2)*pi/180 "в случае если линия параллельна оси абсцисс
if ((a1 = 0) or (a1 = 180)) then
l1a = 1
l1b = 0
l1c = x1
else
l1a = -(a1rad.tan)
l1b = 1
l1c = y1 - (a1rad.tan*x1)
end
if ((a2 = 0) or (a2 = 180)) then
l2a = 1
l2b = 0
l2c = x2
else
l2a = -(a2rad.tan)
l2b = 1
l2c = y2 - (a2rad.tan*x2)
end
D1 = l1a*l2b
D2 = l2a*l1b
D3 = D1 - D2
"Если линии параллельны, в поле результата записываются несуществующие значения
if (D3 = 0) then
resX = 9999
resY = 9999
else resX = ((l1c*l2b) - (l2c*l1b))/D3
resY = ((l1a*l2c) - (l2a*l1c))/D3 end В былые времена я увлекался компьютерной графикой, как 2х так и 3х мерной, в том числе математическими визуализациями. Что называется just for fun, будучи студентом, написал программу визуализирующую N-мерные фигуры, вращающиеся в любых измерениях, хотя практически меня хватило только на определение точек для 4-D гиперкуба. Но это только присказка. Любовь к геометрии осталась у меня с тех пор и по сей день, и я до сих пор люблю решать интересные задачи интересными способами.
Одна из таких задач попалась мне в 2010 году. Сама задача достаточно тривиальна: необходимо найти, пересекаются ли два 2-D отрезка, и если пересекаются - найти точку их пересечения. Более интересно решение, которое, я считаю, получилось достаточно элегантным, и которое я хочу предложить на суд читателя. На оригинальность алгоритма не претендую (хотя и хотелось бы), но в сети подобных решений я найти не смог.
Задача
Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.Решение
Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком.На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются.
Может показаться, что определить, с какой стороны от линии лежит точка - нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты.
Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка. 
Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой.
Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением.
Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию.
Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение.
Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения.
Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(α), и |AB x AD| = |AB||AD| sin(β). |AC|sin(α) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(β) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD"). Так как углы γ и δ - вертикальные углы, то они равны, а значит треугольники PCC" и PDD" подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении.
Имея Z1 (AB x AC, а значит |AB||AC|sin(α)) и Z2 (AB x AD, а значит |AB||AD|sin(β)), мы можем рассчитать CC"/DD" (которая будет равна Z1/Z2), а также зная что CC"/DD" = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:
Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|;
Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;
Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector
1 template
