Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения .

Сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:

Теперь на основе этих формул(свойств), покажем примеры решения логарифмов .

Примеры решения логарифмов на основании формул.

Логарифм положительного числа b по основанию a (обозначается log a b) - это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.

Согласно определения log a b = x, что равносильно a x = b, поэтому log a a x = x.

Логарифмы , примеры:

log 2 8 = 3, т.к. 2 3 = 8

log 7 49 = 2, т.к. 7 2 = 49

log 5 1/5 = -1, т.к. 5 -1 = 1/5

Десятичный логарифм - это обычный логарифм, в основании которого находится 10. Обозначается как lg.

log 10 100 = 2, т.к. 10 2 = 100

Натуральный логарифм - также обычный логарифм логарифм, но уже с основанием е (е = 2,71828... - иррациональное число). Обозначается как ln.

Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.

• Основное логарифмическое тождество
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Логарифм произведения равен сумме логарифмов
  log a (bc) = log a b + log a c

  log 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4

• Логарифм частного равен разности логарифмов
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Свойства степени логарифмируемого числа и основания логарифма

  Показатель степени логарифмируемого числа log a b m = mlog a b

  Показатель степени основания логарифма log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  если m = n, получим log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Переход к новому основанию
  log a b = log c b/log c a,

  если c = b, получим log b b = 1

  тогда log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: " ". Не пропустите!

Если у вас остались вопросы по решению, пишите их в комментариях к статье.

Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.

Определение логарифма

Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b .

Числом е в математике принято обозначать предел, к которому стремиться выражение

Число е является иррациональным числом - числом, несоизмеримым с единицей, оно не может быть точно выраженным ни целым ни дробным рациональным числом.

Буква е - первая буква латинского слова exponere - выставлять напоказ, отсюда в математике название экспоненциальная - показательная функция.

Число е широко применяется в математике, и во всех науках, так или иначе применяющих для своих нужд математические расчеты.

Логарифмы. Свойства логарифмов

Определение: Логарифмом положительного числа b по основанию называется показатель степени с, в которую надо возвести число а, чтобы получить число b.

Основное логарифмическое тождество:

7) Формула перехода к новому основанию:

lna = log e a, e ≈ 2,718…

Задачи и тесты по теме «Логарифмы. Свойства логарифмов»

• Логарифмы — Важные темы для повторения ЕГЭ по математике

Для успешного выполнения заданий по данной теме Вы должны знать определение логарифма, свойства логарифмов, основное логарифмическое тождество, определения десятичного и натурального логарифмов. Основные типы задач по данной теме — это задачи на вычисление и преобразование логарифмических выражений. Рассмотрим их решение на следующих примерах.

Решение: Используя свойства логарифмов, получим

Решение: используя свойства степени, получим

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Свойства логарифмов, формулировки и доказательства.

Логарифмы обладают рядом характерных свойств. В этой статье мы разберем основные свойства логарифмов . Здесь мы дадим их формулировки, запишем свойства логарифмов в виде формул, покажем примеры их применения, а также приведем доказательства свойств логарифмов.

Навигация по странице.

Основные свойства логарифмов, формулы

Для удобства запоминания и использования представим основные свойства логарифмов в виде списка формул. В следующем пункте дадим их формулировки, доказательства, примеры использования и необходимые пояснения.

Свойство логарифма единицы: log a 1=0 для любого a>0 , a≠1 .

Логарифм числа, равного основанию: log a a=1 при a>0 , a≠1 .

Свойство логарифма степени основания: log a a p =p , где a>0 , a≠1 и p – любое действительное число.

Логарифм произведения двух положительных чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
и свойство логарифма произведения n положительных чисел: log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Свойство логарифма частного: , где a>0 , a≠1 , x>0 , y>0 .

Логарифм степени числа: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Следствие: , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Следствие 1: , a>0 , a≠1 , b>0 , b≠1 .

Следствие 2: , a>0 , a≠1 , b>0 , p и q – действительные числа, q≠0 , в частности при b=a имеем .

Формулировки и доказательства свойств

Переходим к формулированию и доказательству записанных свойств логарифмов. Все свойства логарифмов доказываются на основе определения логарифма и вытекающего из него основного логарифмического тождества, а также свойств степени.

Начнем со свойства логарифма единицы . Его формулировка такова: логарифм единицы равен нулю, то есть, log a 1=0 для любого a>0 , a≠1 . Доказательство не вызывает сложностей: так как a 0 =1 для любого a , удовлетворяющего указанным выше условиям a>0 и a≠1 , то доказываемое равенство log a 1=0 сразу следует из определения логарифма.

Приведем примеры применения рассмотренного свойства: log 3 1=0 , lg1=0 и .

Переходим к следующему свойству: логарифм числа, равного основанию, равен единице , то есть, log a a=1 при a>0 , a≠1 . Действительно, так как a 1 =a для любого a , то по определению логарифма log a a=1 .

Примерами использования этого свойства логарифмов являются равенства log 5 5=1 , log 5,6 5,6 и lne=1 .

Логарифм степени числа, равного основанию логарифма, равен показателю степени . Этому свойству логарифма отвечает формула вида log a a p =p , где a>0 , a≠1 и p – любое действительное число. Это свойство напрямую следует из определения логарифма. Заметим, что оно позволяет сразу указать значение логарифма, если есть возможность представить число под знаком логарифма в виде степени основания, подробнее об этом мы поговорим в статье вычисление логарифмов.

К примеру, log 2 2 7 =7 , lg10 -4 =-4 и .

Логарифм произведения двух положительных чисел x и y равен произведению логарифмов этих чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 . Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y , а так как по основному логарифмическому тождеству a log a x =x и a log a y =y , то a log a x ·a log a y =x·y . Таким образом, a log a x+log a y =x·y , откуда по определению логарифма вытекает доказываемое равенство.

Покажем примеры использования свойства логарифма произведения: log 5 (2·3)=log 5 2+log 5 3 и .

Свойство логарифма произведения можно обобщить на произведение конечного числа n положительных чисел x 1 , x 2 , …, x n как log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . Данное равенство без проблем доказывается методом математической индукции.

Например, натуральных логарифм произведения можно заменить суммой трех натуральных логарифмов чисел 4 , e , и .

Логарифм частного двух положительных чисел x и y равен разности логарифмов этих чисел. Свойству логарифма частного соответствует формула вида , где a>0 , a≠1 , x и y – некоторые положительные числа. Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма .

Приведем пример использования этого свойства логарифма: .

Переходим к свойству логарифма степени . Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени. Запишем это свойство логарифма степени в виде формулы: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Сначала докажем это свойство для положительных b . Основное логарифмическое тождество позволяет нам представить число b как a log a b , тогда b p =(a log a b) p , а полученное выражение в силу свойство степени равно a p·log a b . Так мы приходим к равенству b p =a p·log a b , из которого по определению логарифма заключаем, что log a b p =p·log a b .

Осталось доказать это свойство для отрицательных b . Здесь замечаем, что выражение log a b p при отрицательных b имеет смысл лишь при четных показателях степени p (так как значение степени b p должно быть больше нуля, в противном случае логарифм не будет иметь смысла), а в этом случае b p =|b| p . Тогда b p =|b| p =(a log a |b|) p =a p·log a |b| , откуда log a b p =p·log a |b| .

Например, и ln(-3) 4 =4·ln|-3|=4·ln3 .

Из предыдущего свойства вытекает свойство логарифма из корня : логарифм корня n -ой степени равен произведению дроби 1/n на логарифм подкоренного выражения, то есть, , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Доказательство базируется на равенстве (смотрите определение степени с дробным показателем), которое справедливо для любых положительных b , и свойстве логарифма степени: .

Вот пример использования этого свойства: .

Теперь докажем формулу перехода к новому основанию логарифма вида . Для этого достаточно доказать справедливость равенства log c b=log a b·log c a . Основное логарифмическое тождество позволяет нам число b представить как a log a b , тогда log c b=log c a log a b . Осталось воспользоваться свойством логарифма степени: log c a log a b =log a b·log c a . Так доказано равенство log c b=log a b·log c a , а значит, доказана и формула перехода к новому основанию логарифма .

Покажем пару примеров применения этого свойства логарифмов: и .

Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов. Формула перехода к новому основанию логарифма также позволяет в некоторых случаях находить значение данного логарифма, когда известны значения некоторых логарифмов с другими основаниями.

Часто используется частный случай формулы перехода к новому основанию логарифма при c=b вида . Отсюда видно, что log a b и log b a – взаимно обратные числа. К примеру, .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a: .

Осталось доказать свойства сравнения логарифмов.

Воспользуемся методом от противного. Предположим, что при a 1 >1 , a 2 >1 и a 1 2 и при 0 1 справедливо log a 1 b≤log a 2 b . По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2 соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2 , то есть, a 1 ≥a 2 . Так мы пришли к противоречию условию a 1 2 . На этом доказательство завершено.

Основные свойства логарифмов

• Материалы к уроку
• Скачать все формулы

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы - это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами .

Эти правила обязательно надо знать - без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного - все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log a x и log a y . Тогда их можно складывать и вычитать, причем:

Итак, сумма логарифмов равна логарифму произведения, а разность - логарифму частного. Обратите внимание: ключевой момент здесь - одинаковые основания . Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры - и убедитесь:

Задача. Найдите значение выражения: log 6 4 + log 6 9.

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.

Задача. Найдите значение выражения: log 2 48 − log 2 3.

Основания одинаковые, используем формулу разности:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Найдите значение выражения: log 3 135 − log 3 5.

Снова основания одинаковые, поэтому имеем:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные - подобные выражения на полном серьезе (иногда - практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

• log a x n = n · log a x ;
• 
• 

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить - в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log 7 49 6 .

Избавимся от степени в аргументе по первой формуле:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

[Подпись к рисунку]

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели - получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log 2 7. Поскольку log 2 7 ≠ 0, можем сократить дробь - в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

В частности, если положить c = x , получим:

[Подпись к рисунку]

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log 5 16 · log 2 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log 9 100 · lg 3.

Основание и аргумент первого логарифма - точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

1. n = log a a n

2. В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

   Вторая формула - это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.

   В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз - многие на нем «зависают».

   Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

   [Подпись к рисунку]

   Заметим, что log 25 64 = log 5 8 - просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

   [Подпись к рисунку]

   Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

   Логарифмическая единица и логарифмический ноль

   В заключение приведу два тождества, которые сложно назвать свойствами - скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

   1. log a a = 1 - это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
   2. log a 1 = 0 - это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица - логарифм равен нулю! Потому что a 0 = 1 - это прямое следствие из определения.

   Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее - и решайте задачи.

   Логарифм. Свойства логарифма (сложение и вычитание).

   Свойства логарифма вытекают из его определения. И так логарифм числа b по основанию а определяется как показатель степени, в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).

   Из данной формулировки следует, что вычисление x=log a b , равнозначно решению уравнения a x =b. Например, log 2 8 = 3 потому, что 8 = 2 3 . Формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа.

   С логарифмами, как и с любыми числами, можно выполнять операции сложения, вычитания и всячески трансформировать. Но ввиду того, что логарифмы — это не совсем ординарные числа, здесь применимы свои особенные правила, которые называются основными свойствами .

   Сложение и вычитание логарифмов.

   Возьмем два логарифма с одинаковыми основаниями: log a x и log a y . Тогда сними возможно выполнять операции сложения и вычитания:

   Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов — логарифму частного. Причем это верно если числа а , х и у положительны и а ≠ 1.

   Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!

   Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.

   Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а , x и у положительны и а ≠ 1 , то:

   Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а , х и у положительны и а ≠ 1 , то:

   Применим вышеизложенные теоремы для решения примеров :

   Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:

   так как выражения log 2 (-8) и log 2 (-4) вообще не определены (логарифмическая функция у = log 2 х определена лишь для положительных значений аргументах ).

   Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x 1 , x 2 , . . . ,x n существует тождество:

   Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что log a 1= 0, следовательно,

   А значит имеет место равенство:

   Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:

   Логарифм. Свойства логарифмов

   Логарифм. Свойства логарифмов

   Рассмотрим равенство . Пусть нам известны значения и и мы хотим найти значение .

   То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

   Пусть переменная может принимать любое действительное значение, тогда на переменные и накладываются такие ограничения: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   Если нам известны значения и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое действие, которое называется логарифмирование .

   Чтобы найти значение , мы берем логарифм числа по основанию :

   Логарифмом числа по основанию называется показатель степени, в которую надо возвести , чтобы получить .

   То есть основное логарифмическое тождество :

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   является по сути математической записью определения логарифма .

   Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

   Перечислим основные свойства логарифмов :

   (o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=»d1″/>

   4.

   5.

   Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:

   6.

   7.

   8.

   9.

   Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию :

   10.

   12. (следствие из свойства 11)

   

   Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

   13.

   14.

   15.

   Частные случаи:

   — десятичный логарифм

   — натуральный логарифм

   При упрощении выражений, содержащих логарифмы применяется общий подход:

   1. Представляем десятичные дроби в виде обыкновенных.

   2. Смешанные числа представляем в виде неправильных дробей.

   3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.

   4. Стараемся привести все логарифмы к одному основанию.

   5. Применяем свойства логарифмов.

   Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.

   Пример 1.

   Вычислить:

   Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.

   ==(по свойству 7)=(по свойству 6) =

   Подставим показатели, которые у нас получились в исходное выражение. Получим:

   Ответ: 5,25

   Пример 2. Вычислить:

   

   Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

   Разложим числа, стоящие под знаком логарифма на простые множители:

   Применим свойства 4 и 6:

   Введем замену

   Получим:

   Ответ: 1

   Логарифм . Основное логарифмическое тождество.

   Свойства логарифмов. Десятичный логарифм. Натуральный логарифм.

   Логарифмом положительного числа N по основанию (b > 0, b 1) называется показатель степени x , в которую нужно возвести b , чтобы получить N .

   Эта запись равнозначна следующей: b x = N .

   П р и м е р ы: log 3 81 = 4 , так как 3 4 = 81 ;

   log 1/3 27 = – 3 , так как (1/3) — 3 = 3 3 = 27 .

   Вышеприведенное определение логарифма можно записать в виде тождества:

   

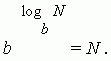
   Основные свойства логарифмов.

   2) log 1 = 0 , так как b 0 = 1 .

   3) Логарифм произведения равен сумме логарифмов сомножителей:

   4) Логарифм частного равен разности логарифмов делимого и делителя:

   5) Логарифм степени равен произведению показателя степени на логарифм её основания:

   Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:

   

   6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак лога рифма:

   

   Два последних свойства можно объединить в одно:

   

   7) Формула модуля перехода (т. e . перехода от одного основания логарифма к другому основанию):

   

   В частном случае при N = a имеем:

   

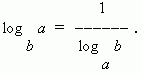
   Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, . p авны соответственно 1, 2, 3, …, т.е. имеют столько положительных

   единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001, . p авны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей (считая и нуль целых). Логарифмы остальных чисел имеют дробную часть, называемую мантиссой . Целая часть логарифма называется характеристикой . Для практического при менения десятичные логарифмы наиболее удобны.

   Натуральным логарифмом называется логарифм по основанию е . Он обозначается ln , т.е. log e N = ln N . Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число (1 + 1 / n ) n при неограниченном возрастании n (см. первый замечательный предел на странице «Пределы числовых последовательностей»).
   Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию.

• Что нужно сегодня для усыновления ребенка в России? Усыновление в России, кроме ответственного личного решения, предполагает ряд процедур государственной проверки кандидатов. Жесткий отбор на подготовительном этапе способствует более […]
• Сведения бесплатно по ИНН или ОГРН из реестра налоговой по всей России - онлайн На Едином портале Налоговых услуг могут быть получены сведения о государственной регистрации юридических лиц, индивидуальных предпринимателей, […]
• Наказание за езду без документов (водительские права, страховка, СТС) Иногда по забывчивости водители садятся за руль без ВУ и получают штраф за езду без документов. Напомним, что автолюбитель за рулём при себе в обязательном порядке […]
• Цветы мужчин. Какие цветы можно подарить мужчине? Какие цветы мужчине можно подарить? «Мужских» цветов не так много, но есть такие, которые дарят мужчинам. Маленький цветочный список перед вами: Хризантемы. Розы. Гвоздики. […]
• Служебная записка – это специальная форма документа, которая используется во внутренней среде предприятия и служит для быстрого решения текущих производственных проблем. Обычно этот документ составляется с целью внесения какого-либо […]
• Когда и как получить накопительную часть пенсии в Сбербанке? Сбербанк является банком-партнером государственного пенсионного фонда. На основании этого граждане, оформившие накопительную пенсию, могли переводить в него накопительную часть […]
• Детские пособия в Ульяновске и Ульяновской области в 2018 году Кроме того, во всех субъектах работают программы, утвержденные федеральным законодательством. Разберем, кто и на какие льготы может рассчитывать. Как региональные власти […]
• Подробное руководство, как составить доверенность на представление интересов физического лица в суде В гражданском или арбитражном иске, в административном или уголовном деле интересы и истца, и ответчика могут представляться поверенным: […]

Рассмотрим уравнение a x = b, при a > 0 и a не равном единице. Это уравнение не имеет решений при b меньшем либо равным нулю. И имеет единственное решение при b > 0. Данное решение называют логарифмом b по основанию a b и обозначают следующим образом:

log a (b)

Логарифмом числа b по основанию f называется показатель степени , в которую необходимо возвести число а, чтобы получилось число b.

a (log a (b)) = b.

Данная формула называется основным логарифмическим тождеством . Она верна для любого положительного не равного единице a, и любого положительного b.

Примеры логарифмов

Рассмотрим несколько примеров:

1. Найти значение log 2 (32). 32 можно представить как 2 5 . То есть для того, чтобы нам получить число 32, необходимо двойку возвести в пятую степень. Следовательно, log 2 (32) = 5.

2. Найти логарифм числа 1/9 по основанию √3. Так как (√3) 4 = 1/9, получаем, что log √3 (1/9) = -4.

3. Найти х такое, что будет верно неравенство: log 8 (x) = 1/3. Применим основное логарифмическое тождество:

x = 8 (log 8 (x)) = 8 (1/8) = 2.

Свойства логарифмов

У логарифмов есть несколько свойств, которые прямо следуют из свойств показательной функции. Основные свойства логарифмов:

1. log a (1) = 0;

2. log a (a) = 1;

3. log a (x*y) = log a (x) + log a (x) - логарифм произведения равен сумме логарифмов;

4. log x (x/y) = log a (x) - log a (y) - логарифм частного равен разности логарифмов;

5. log a (x p) = p* log a (x) - логарифм степени будет равен произведению показателя степени на логарифм основания этой степени.

Приведенные выше свойства будут справедливы для любого положительного числа а , не равного единице, любых положительны x и y, и любого действительного p.

Для логарифмов существует формула перехода к новому основанию:

log a (x) = (log b (x))/(log b (a)).

Данная формула будет иметь смысл лишь в том случае, когда обе её части будут иметь смысл. То есть должны выполняться следующие условия:

x > 0, a > 0,b > 0, a не равно единице, b не равно единице.

Логарифмы основанием которых является число 10, называются десятичными логарифмами . Логарифмы, основанием которых является число e, называются натуральными логарифмами .

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) "b" по его основанию "a" считается степень "c", в которую необходимо возвести основание "a", чтобы в итоге получить значение "b". Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное - понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание "a" всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь "1" и "0" в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и "с" должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел - это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени - это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема "логарифмы". Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 - оно является логарифмическим неравенством, так как неизвестное значение "х" находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример - логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула "свойством степени логарифма". Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов - примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы "Натуральные логарифмы".

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Продолжаем изучать логарифмы. В этой статье мы поговорим про вычисление логарифмов , этот процесс называют логарифмированием . Сначала мы разберемся с вычислением логарифмов по определению. Дальше рассмотрим, как находятся значения логарифмов с использованием их свойств. После этого остановимся на вычислении логарифмов через изначально заданные значения других логарифмов. Наконец, научимся использовать таблицы логарифмов. Вся теория снабжена примерами с подробными решениями.

Навигация по странице.

Вычисление логарифмов по определению

В простейших случаях возможно достаточно быстро и легко выполнить нахождение логарифма по определению . Давайте подробно рассмотрим, как происходит этот процесс.

Его суть состоит в представлении числа b в виде a c , откуда по определению логарифма число c является значением логарифма. То есть, нахождению логарифма по определению отвечает следующая цепочка равенств: log a b=log a a c =c .

Итак, вычисление логарифма по определению сводится к нахождению такого числа c , что a c =b , а само число c есть искомое значение логарифма.

Учитывая информацию предыдущих абзацев, когда число под знаком логарифма задано некоторой степенью основания логарифма, то можно сразу указать, чему равен логарифм – он равен показателю степени. Покажем решения примеров.

Пример.

Найдите log 2 2 −3 , а также вычислите натуральный логарифм числа e 5,3 .

Решение.

Определение логарифма позволяет нам сразу сказать, что log 2 2 −3 =−3 . Действительно, число под знаком логарифма равно основанию 2 в −3 степени.

Аналогично находим второй логарифм: lne 5,3 =5,3 .

Ответ:

log 2 2 −3 =−3 и lne 5,3 =5,3 .

Если же число b под знаком логарифма не задано как степень основания логарифма, то нужно внимательно посмотреть, нельзя ли прийти к представлению числа b в виде a c . Часто такое представление бывает достаточно очевидно, особенно когда число под знаком логарифма равно основанию в степени 1 , или 2 , или 3 , ...

Пример.

Вычислите логарифмы log 5 25 , и .

Решение.

Несложно заметить, что 25=5 2 , это позволяет вычислять первый логарифм: log 5 25=log 5 5 2 =2 .

Переходим к вычислению второго логарифма . Число можно представить в виде степени числа 7 : (при необходимости смотрите ). Следовательно, .

Перепишем третий логарифм в следующем виде . Теперь можно увидеть, что , откуда заключаем, что . Следовательно, по определению логарифма .

Коротко решение можно было записать так: .

Ответ:

log 5 25=2 , и .

Когда под знаком логарифма находится достаточно большое натуральное число, то его не помешает разложить на простые множители. Это часто помогает представить такое число в виде некоторой степени основания логарифма, а значит, вычислить этот логарифм по определению.

Пример.

Найдите значение логарифма .

Решение.

Некоторые свойства логарифмов позволяют сразу указать значение логарифмов. К таким свойствам относятся свойство логарифма единицы и свойство логарифма числа, равного основанию: log 1 1=log a a 0 =0 и log a a=log a a 1 =1 . То есть, когда под знаком логарифма находится число 1 или число a , равное основанию логарифма, то в этих случаях логарифмы равны 0 и 1 соответственно.

Пример.

Чему равны логарифмы и lg10 ?

Решение.

Так как , то из определения логарифма следует .

Во втором примере число 10 под знаком логарифма совпадает с его основанием, поэтому десятичный логарифм десяти равен единице, то есть, lg10=lg10 1 =1 .

Ответ:

И lg10=1 .

Отметим, что вычисление логарифмов по определению (которое мы разобрали в предыдущем пункте) подразумевает использование равенства log a a p =p , которое является одним из свойств логарифмов.

На практике, когда число под знаком логарифма и основание логарифма легко представляются в виде степени некоторого числа, очень удобно использовать формулу , которая соответствует одному из свойств логарифмов. Рассмотрим пример нахождения логарифма, иллюстрирующий использование этой формулы.

Пример.

Вычислите логарифм .

Решение.

Ответ:

.

Не упомянутые выше свойства логарифмов также используются при вычислении, но об этом поговорим в следующих пунктах.

Нахождение логарифмов через другие известные логарифмы

Информация этого пункта продолжает тему использования свойств логарифмов при их вычислении. Но здесь основное отличие состоит в том, что свойства логарифмов используются для того, чтобы выразить исходный логарифм через другой логарифм, значение которого известно. Приведем пример для пояснения. Допустим, мы знаем, что log 2 3≈1,584963 , тогда мы можем найти, например, log 2 6 , выполнив небольшое преобразование с помощью свойств логарифма: log 2 6=log 2 (2·3)=log 2 2+log 2 3≈ 1+1,584963=2,584963 .

В приведенном примере нам было достаточно использовать свойство логарифма произведения. Однако намного чаще приходится применять более широкий арсенал свойств логарифмов, чтобы вычислить исходный логарифм через заданные.

Пример.

Вычислите логарифм 27 по основанию 60 , если известно, что log 60 2=a и log 60 5=b .

Решение.

Итак, нам нужно найти log 60 27 . Несложно заметить, что 27=3 3 , и исходный логарифм в силу свойства логарифма степени можно переписать как 3·log 60 3 .

Теперь посмотрим, как log 60 3 выразить через известные логарифмы. Свойство логарифма числа, равного основанию, позволяет записать равенство log 60 60=1 . С другой стороны log 60 60=log60(2 2 ·3·5)= log 60 2 2 +log 60 3+log 60 5= 2·log 60 2+log 60 3+log 60 5 . Таким образом, 2·log 60 2+log 60 3+log 60 5=1 . Следовательно, log 60 3=1−2·log 60 2−log 60 5=1−2·a−b .

Наконец, вычисляем исходный логарифм: log 60 27=3·log 60 3= 3·(1−2·a−b)=3−6·a−3·b .

Ответ:

log 60 27=3·(1−2·a−b)=3−6·a−3·b .

Отдельно стоит сказать о значении формулы перехода к новому основанию логарифма вида . Она позволяет от логарифмов с любыми основаниями переходить к логарифмам с конкретным основанием, значения которых известны или есть возможность их отыскать. Обычно от исходного логарифма по формуле перехода переходят к логарифмам по одному из оснований 2 , e или 10 , так как по этим основаниям существуют таблицы логарифмов, позволяющие с определенной степенью точности вычислять их значения. В следующем пункте мы покажем, как это делается.

Таблицы логарифмов, их использование

Для приближенного вычисления значений логарифмов могут быть использованы таблицы логарифмов . Наиболее часто используется таблица логарифмов по основанию 2 , таблица натуральных логарифмов и таблица десятичных логарифмов. При работе в десятичной системе счисления удобно пользоваться таблицей логарифмов по основанию десять. С ее помощью и будем учиться находить значения логарифмов.

Представленная таблица позволяет с точностью до одной десятитысячной находить значения десятичных логарифмов чисел от 1,000 до 9,999 (с тремя знаками после запятой). Принцип нахождения значения логарифма с помощью таблицы десятичных логарифмов разберем на конкретном примере – так понятнее. Найдем lg1,256 .

В левом столбце таблицы десятичных логарифмов находим две первые цифры числа 1,256 , то есть, находим 1,2 (это число для наглядности обведено синей линией). Третью цифру числа 1,256 (цифру 5 ) находим в первой или последней строке слева от двойной линии (это число обведено красной линией). Четвертую цифру исходного числа 1,256 (цифру 6 ) находим в первой или последней строке справа от двойной линии (это число обведено зеленой линией). Теперь находим числа в ячейках таблицы логарифмов на пересечении отмеченной строки и отмеченных столбцов (эти числа выделены оранжевым цветом). Сумма отмеченных чисел дает искомое значение десятичного логарифма с точностью до четвертого знака после запятой, то есть, lg1,236≈0,0969+0,0021=0,0990 .

А можно ли, используя приведенную таблицу, находить значения десятичных логарифмов чисел, имеющих больше трех цифр после запятой, а также выходящих за пределы от 1 до 9,999 ? Да, можно. Покажем, как это делается, на примере.

Вычислим lg102,76332 . Сначала нужно записать число в стандартном виде : 102,76332=1,0276332·10 2 . После этого мантиссу следует округлить до третьего знака после запятой, имеем 1,0276332·10 2 ≈1,028·10 2 , при этом исходный десятичный логарифм приближенно равен логарифму полученного числа, то есть, принимаем lg102,76332≈lg1,028·10 2 . Теперь применяем свойства логарифма: lg1,028·10 2 =lg1,028+lg10 2 =lg1,028+2 . Наконец, находим значение логарифма lg1,028 по таблице десятичных логарифмов lg1,028≈0,0086+0,0034=0,012 . В итоге весь процесс вычисления логарифма выглядит так: lg102,76332=lg1,0276332·10 2 ≈lg1,028·10 2 = lg1,028+lg10 2 =lg1,028+2≈0,012+2=2,012 .

В заключение стоит отметить, что используя таблицу десятичных логарифмов можно вычислить приближенное значение любого логарифма. Для этого достаточно с помощью формулы перехода перейти к десятичным логарифмам, найти их значения по таблице, и выполнить оставшиеся вычисления.

Для примера вычислим log 2 3 . По формуле перехода к новому основанию логарифма имеем . Из таблицы десятичных логарифмов находим lg3≈0,4771 и lg2≈0,3010 . Таким образом, .

Список литературы.

• Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 - 11 классов общеобразовательных учреждений.
• Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).